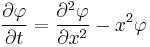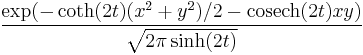Mehler kernel
In mathematics, the Mehler kernel is the heat kernel of the Hamiltonian of the harmonic oscillator. Mehler (1866) gave an explicit formula for it called Mehler's formula. The Kibble–Slepian formula generalizes Mehler's formula to higher dimensions.
The Mehler kernel φ(x, y, t) is a solution to
Mehler's kernel is
This can also be written as an infinite series involving Hermite polynomials of x and y.
References
- Grigor'yan, Alexander (2009), Heat kernel and analysis on manifolds, AMS/IP Studies in Advanced Mathematics, 47, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-4935-4, MR2569498, http://books.google.com/books?id=X7QQcVa2EWsC
- Mehler, F. G. (1866), "Ueber die Entwicklung einer Function von beliebig vielen Variabeln nach Laplaceschen Functionen höherer Ordnung" (in German), Journal für Reine und Angewandte Mathematik (66): 161–176, ISSN 0075-4102, JFM 066.1720cj, http://resolver.sub.uni-goettingen.de/purl?GDZPPN002152975